Thursday, July 4th 2013
The Headwaters British Car Club had a notice on their web site about a
get together to drive up the old hill climb route used in competitions
in the 1950's and early 60's. Since my '59 Plus 4 is feeling much
better after some fettling by the Beer brothers in Bolton I decided to
crash the hill climb party. The weather looked iffy, but the radar map
showed just the minimum precipitation rate so I went for it. Half of my
trip was on the highway so with no traffic jam I managed to drive dry
through the last of the drizzle. By the time I got up to Hockley Vally
Road and 3rd Line the sun was out. I wasn't the only party crasher, a
group from Collingwood drove in after I did giving a total of 26 cars.
Three of the cars at the recreation were driven in races on the hill
back in its day, a MG racer and the Sands' Morgan and Allard.
You can see what the original event looked like in a video on this web
page of the 'In the Hills' magazine:
http://www.inthehills.ca/2013/06/current/a-classic-love-story/#hillClimb
Now days the bridge is wider and the hedge rows have grown thicker.
Not only were there cars that had raced on the hill but also drivers who
had competed here. Some driving like Al Sands and some as spectators.
Bob Crossan approached me when I got back down the hill and kindly gave
me copies of two photographs of him competing in his '53 Plus 4.
The weather on the trip home started to look ominous as I passed through
Brampton on the 410 but a traffic jam provided enough of a delay that
the worst of it moved east of my route before I got to it. So I got
home with just some road spray all over the outside of the car.
Friday, 5 July 2013
Thursday, 4 July 2013
I'm saying goodbye to an old friend: My Morgan
 |
| Still looking good after almost 45 years. (A tip of the hat to Steve and Martin Beer.) |
I have owned two Morgans in my lifetime. One came from Malvern Link while the other came from Bolton, Ontario. And both were the same car!
My Malvern-Link-Morgan could not be driven from Windsor to Ann Arbour on a hot summer's day without overheating. I learned to carry gallon jugs of water any time I ventured outside the city. That car seemed to run on water along with gasoline.
 |
| Mississippi: a place to party in the late 60s. Ah, the memories. |
More than once I was stopped for traveling over the speed limit. I would explain the little roadster shook at highway speed, some kind of resonance I would say. The police officer would invariably tell me that traveling a bit under the speed limit would also solve the problem. I never got a ticket, or I should say the Morgan never got a ticket. Everyone, even the traffic police, loved that car.
Starting was hit and miss with my first Morgan. I learned to read a parking lot. I always noted the placement of the storm drain and parked accordingly. I got quite adept at pushing my Morgan towards the drain, hopping in and popping the clutch. As the engine was already hot, this little trick always got the little car running. (Although Curly at Metro Motors in Windsor gets credit for curing my Mog of this problem. Thanks to the changes he had made to my car, it started one winter's morning in Kapuskasing, Ontario, despite the temp nearing 40 below.) The Beers have improved on Curly's work. I now park where I please and storm drains be damned.
My Bolton, Ontario, Morgan never overheats. O.K., I confess it overheated once in California on a very hot day after a long, fast run but the water was captured in an overflow bottle — also new with my Bolton redo.
If I let the temperature gauge control my speed, the car never overheats. Never. The water jugs are now just memories.
As for shake, the Bolton Morgan is rock solid. I credit the 72-spoke rims. I haven't had to talk my way out of a speeding ticket since the Beers redid my car. The little roadster is a joy at 50 mph, 60 mph and 70 mph, even if the rpm's are a little high at 70 mph. (Night is the best time for traveling fast. The air is cooler and it is more important in the dark to be keeping up with the flow of traffic. And, let's be honest, the glow of the dash lights is just so cool in the dark of night.)
 |
| Judy and I on our way back from the west coast in 2010. |
In the end, the little car outlasted me. I am not up to the journey. In the past month, I have had a number of shocks from the ICD I carry in my chest. I have had at least two TIA incidents, minor strokes, I have stopped driving until I get the all-clear from my doctors.
 |
| Fiona: "A Morgan is NOT a Miata." |
My three-year-old granddaughter, Fiona, is taking it hard. When a relative tried cheering her up by saying, "Maybe grandpa Ken will buy a Miata. They come with an automatic and grandma Judy can drive it." Fiona replied firmly: "A Miata is NOT a Morgan."
Monday, 4 March 2013
London (Ontario) Weekend_Mar. 12, 2013 update
The Morgan Sports Car Club June run to the Fleetwood Country Cruize-In is on. Cost:
- $82.49 : Accommodation starts at $82.49 per couple per night (two couples to a suite, two nights occupancy)
- $59 : Where The Action Is tour Friday night with food and beer available
- $10 : per person admittance to Fleetwood Country Cruize-In Saturday
Dates: Friday, June 7th to Sunday, June 9th
Hotel: Marriott Residence Inn, downtown London
Originally an apartment complex, the building was converted to an inn during construction. This explains the extra large rooms in the three suites being held for the club.
Each suite offers two bedrooms, each with a king sized bed. There are two bathrooms. $113.57 per night per couple based on two couples sharing the suite. (This price includes underground parking.)
Similar suites, smaller with one bathroom rather than two, are available for $82.49 per night per couple based on two couples sharing the suite. (This price includes underground parking.)
The inn allows pets but asks to be informed in advance. There is a $75 flat charge (to cover cleaning.)
To reserve a suite: Please call the Marriott Residence Inn at (519) 433-7222. Tell them you are part of the Morgan Sports Car Club of Canada group in order to get the best rate. Find a couple with whom to share the suite and please call ASAP. The inn is holding three of the top end suites for us for 30 days. The lesser suites are available on a first come-first serve basis.
Each suite also offers a pull-out sofa bed.
Complimentary Guest Amenities include but are not restricted to:
- Hot Buffet Breakfast
- Daily Newspapers - Globe & Mail, London Free Press & USA Today
- Cozy Hearth Room with television & games for socializing and relaxing
- Complimentary entry to an indoor track and swimming pool
Judy and I live only 15 minutes from the Marriott. Plunkett's is only 5 minutes west of our place.
Event: Steve Plunkett Fleetwood Country Cruize-In (Said to be the largest outdoor car show on the planet.)
Friday evening: The Where The Action Is tour is Friday night featuring —
- Mary Wilson of the Supremes
- The Association
- Paul Revere and the Raiders
- Mitch Ryder
Tickets $59: Tickets to the Friday night Fleetwood Country Cruize-In kick-off show are $59 plus tax if paid for in cash and picked up at the downtown ticket office. Contact Ken Wightman (londondailyphoto1@gmail.com) and Ken will pick up your tickets, reimburse him later. Three couples already have tickets.
Mary Wilson sings lead with the Supremes on this cover of Come And Get These Memories. Ken has caught Mary Wilson in the past and she never disappoints. The young and oh-so-talented teen who escaped Detroit's Douglass Brewster projects thanks to her singing talent has never lost the sparkle that made her an early MoTown star.
Rob Fournie, who has already bought his tickets, caught Paul Revere and the Raiders some years ago. He assures me they put on a great show. Fine entertainers.
I feel confident The Association will also be a winner. Mitch, Devil-with-a-Blue-Dress, Ryder is the fourth and last act on the ticket. Plunkett is well known starting his weekends with a blow-out Friday night. Plunkett loves old Caddies and old rock 'n' roll and it shows.
 |
| The Amphicars will be there again offering rides. |
Read about a previous Plunkett Fleetwood Cruize Event:
Cars the Stars at Fleetwood Country Cruize-In
Saturday night is a BBQ at the Wightman's (rain or shine.)
Sunday: In the morning there will be a run, the exact route TBA. Lunch may be in the Pinecroft Green Frog Tea Room again. After lunch it will be time to head east and home.
I have opened this page on the MSCCC blog to keep everyone up-to-date on the London Event. Direct all questions to Ken Wightman at 519-657-3779 or e-mail Ken at: londondailyphoto1@gmail.com.
Cheers,
Ken
Sunday, 10 February 2013
Wooden Trike World Tour
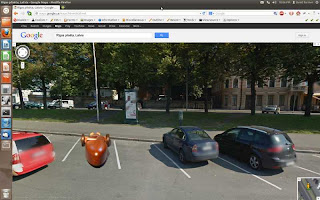
I installed a statistics package on the MSCCC web site back in December. One of the curious things I learned from it is that the build of the new Morgan three wheeler model attracts a lot of attention from all around the globe. Roughly every other day someone looks at a couple of pages or more. I decided to take a look at their towns with Google Street View. So here is my thank you for all the interest in the model trike.
Andover Massachusetts: If any of you do build a model please send pictures and I'll add a gallery page to the series on the trike.
http://morgansportscarclubofcanada.com/New3WheelerIndex.php
Send pictures to morgansportscarclubofcanada@gmail.com
Andover Massachusetts: If any of you do build a model please send pictures and I'll add a gallery page to the series on the trike.
http://morgansportscarclubofcanada.com/New3WheelerIndex.php
Send pictures to morgansportscarclubofcanada@gmail.com
Tuesday, 5 February 2013
More Morgan Models
I found another, from scratch, Morgan model maker who builds wire model cars.
A three wheeler:
A 4/4 (ignore the '+8' in the video's title):
They have several others from a Bugatti Coupe 57S to a Fiat 500:
A three wheeler:
A 4/4 (ignore the '+8' in the video's title):
They have several others from a Bugatti Coupe 57S to a Fiat 500:
Sunday, 13 January 2013
Designing Wooden Model Wire Wheels (Part 2)
The wire wheels that I see on Morgans have the spokes that attach to opposite ends of the hub cross between each other before they attach to the rim. This is a little more complex than the motorcycle style wheels I made for the 3 Wheeler model (http://morgansportscarclubofcanada.com/New3WheelerIndex.php) where all the spokes attach to the rim along its centre line. In my POVray model for designing the wheel I'll put in a value to set how far from and to which side of the centre line the spokes will attach to the rim.
When I designed the 3 Wheeler's wheels I did a lot of fiddling with the positioning of where the spokes go into the hub. Since this time I will be fiddling with the rim end already I decided to calculate where the spoke should go in the hub. The objective is to put the spoke as near as possible to the end of the hub without letting the hole for holding the tip of the spoke go through the end of the hub.
In the following picture the black coordinate system is the one POVray will use when building the wheel. I also added a second set of coordinates in red to make life easier while calculating the y coordinates of the ends of the spokes. The red system's y-axis goes through the point where a spoke enters the hub, like we calculated last week. The whole system is rotated so the x-axis crosses the point where the spoke enters the rim, also calculated last week. Then the coordinates are shifted up or down in the y direction as required to have the x-axis enter the rim at the same point the topside of the spoke enters the hub. We use the side of the spoke here not its centre line as the side will be first to reach the end of the hub.
Here is a cut-away to show how the red coordinates line up with the spoke.
What I want to calculate is the angle between the spoke and the x-axis.
I know the distance from the origin to where the x-axis enters the rim, apply the Pythagorean theorem to the points calculated last week. Call it d.
I will set the depth of the hole in the hub for the tip of the spoke. Call it t.
And for each run I will enter the y coordinate for where the top side of the spoke enters the rim. Then the distance from the origin up the y-axis to the top of the hub is one half the distance between the ends of the hub minus the input value of y for the spoke at the rim. Call it h.
The next diagram takes the x-y plane from the red coordinates in the cut-away diagram and adds in a short segment of the line across the end of the hub, line y = h, and the line along the top side of the spoke, line ACB. Under it is the derivation of a trigonometric formula for the angle of the spoke.
I labeled the picture of the wheel with the points in the geometry diagram.
A - is on the inside of the rim where the top of the spoke enters the rim
B - is on the face of end of the hub where the spoke would break out of the hub
D - is at the outer circumference on the end of the hub
C - is on the side of the hub where the top of the spoke enters the hub
O - is on the side of the hub, its distance from the end of the hub is variable as I try different amounts of cross over between the outside and inside sets of spokes. It is input as the y coordinate in the POVray coordinates where the top side of the spoke enters the rim.
The distance from O to A we have from last week's work. We calculated the coordinates of the spoke's end points on the plane, use the Pythagorean theorem to calculate the distance, 'd', between them.
d = SQRT((Xrim - Xhub)^2 + (Zrim - Zhub)^2)
The distance from O to D is one half the hub length minus the y coordinate of the offset at the rim. If the offset is to -1/8" and the hub is 1/2" long then this height , h = 1/2 * 1/2 -(-1/8) = 3/8".
The distance B to C, t, is set to 1/32".
What I'm after is the angle OAC which will also be needed in designing the jig for drilling the spoke holes. I think I've broken down the steps fine enough in the diagram for you to follow how I got my formula for the angle. Lets rename angle OAC as just 'a' so the formula reads:
d * tan(a) + t * sin(a) - h = 0
I poked around on http://mathworld.wolfram.com and some other math sites for a solution to this equation but trigonometric equations do not often have easy solutions. This was not one of the easy ones. Having been programming computers for over 40 years I thought of building a binary search program, but in case there was something better I asked for help on the Google group mog-group. Brent Meeker responded with two possibilities. The first idea involved using some trigonometric transformations to eliminate the tan(a) and turn this equation into a quartic equation in sin(a). After looking at the Wolfram site's instructions for solving a quartic equation I had to agree with Brent that this is not the way to do it. His better idea is an iterative approach called, fixed point iteration.
Starting with the fact that tan(a) = sin(a)/cos(a) Brent reworked my formula to calculate the error in a guess of the answer. Here I just paste his explanation.
Instead guess a value of a and solve for the amount of error e in your guess. First multiply thru by cos so you have
d*sin(a) - h*cos(a) + t*sin(a)cos(a) =0
or using a trig identity
d*sin(a) - h*cos(a) + 0.5*t*sin(2a) =0
Then substitute in your guess which is (a-e)
d*sin(a-e) - h*cos(a-e) + 0.5*t*sin(2a-2e) =0
or using trig identities
d*[sin(a)cos(-e)+cos(a)sin(-e)] - h*[cos(a)cos(-e)-sin(a)sin(-e)] +
0.5*t*[sin(2a)cos(-2e)+sin(-2e)cos(2a)]=0
And then here's the payoff. For small angles e, sin(e)=e and cos(e)=1. So you assume you're close and e is small so the above equation becomes
d*[sin(a) -e*cos(a)] - h*[cos(a)+e*sin(a)] + 0.5*t*[sin(2a)-2e*cos(2a)]=0
Which you easily solve for e.
e={d*sin(a) - h*cos(a) + 0.5*t*sin(2a)}/{cos(a) + h*sin(a) +t*cos(2a)}
You add this value to your estimate, which was a-e, and you will have a new value much closer to the true value of a. Take this new value as a new guess and repeat the above calculation of a new e. This should converge very quickly to as much accuracy as you need.
I tried this in a spreadsheet with d = 0.5, h = 0.35, t = 0.03, and a first guess of 45 degrees. But I found I needed to subtract e from the guess not add, maybe because POVray's angles turn backwards to the mathematical convention.
a e
45 17.8768435793
27.1231564207 2.2868135347
24.836342886 0.4709482886
24.3653945974 0.0993094122
It homed in to greater accuracy than any protractor I have in just 4 steps. And it can be coded in a simple while loop containing just two lines of code.
Now that I have the angle a, we can find the point C, it is t * sin(a) in from the end of the hub. But to draw this spoke we need its centre line, line AC is on the side of the spoke.
Adding the spoke centre line to the diagram we can calculate how far it is down to the centre.
The centre line is {Spoke Radius / cos(a)} below the line AC.
Now we can calculate POVray's Y coordinates for the spoke. At the hub it will be
Yhub = 0.5 * Hub Width - t * sin(a) - Spoke Radius / cos(a)
At the rim it will be
Yrim = The input Offset from Centre - Spoke Radius / cos(a)
Of course the spokes on the other side of the hub will have some signs changed. At the hub it will be
Yhub = -0.5 * Hub Width + t * sin(a) + Spoke Radius / cos(a)
and at the rim
Yrim = The input Offset from Centre + Spoke Radius / cos(a)
Now we have the x, y, and z coordinates for the ends of the outer sets of spokes. The inner sets which cross behind the outer ones will have the same angle to the plane of the wheel as their pair mates. To avoid hitting their mates they must be inset by at least:
Spoke Diameter / cos(a)
This amount works OK for the spokes on the narrow end with their shallow angle but I had to increase the inset on the other end's more steeply angled spokes, 1.1 times did the trick. POVray's intersect function clearly shows where any spokes intersect. After playing with the offsets at the rim to get no intersect pieces showing I removed the intersect function to make the following stereoscopic picture of the wheel.
Look through this picture to merge the images and get the 3D effect. It may help to thumb your nose at the picture so each eye see only the image on its side and/or shrink the picture's window a little.
I see I will have to bevel the corner where the hub widens so the spokes from the narrow end can clear it.
When I designed the 3 Wheeler's wheels I did a lot of fiddling with the positioning of where the spokes go into the hub. Since this time I will be fiddling with the rim end already I decided to calculate where the spoke should go in the hub. The objective is to put the spoke as near as possible to the end of the hub without letting the hole for holding the tip of the spoke go through the end of the hub.
In the following picture the black coordinate system is the one POVray will use when building the wheel. I also added a second set of coordinates in red to make life easier while calculating the y coordinates of the ends of the spokes. The red system's y-axis goes through the point where a spoke enters the hub, like we calculated last week. The whole system is rotated so the x-axis crosses the point where the spoke enters the rim, also calculated last week. Then the coordinates are shifted up or down in the y direction as required to have the x-axis enter the rim at the same point the topside of the spoke enters the hub. We use the side of the spoke here not its centre line as the side will be first to reach the end of the hub.
Here is a cut-away to show how the red coordinates line up with the spoke.
What I want to calculate is the angle between the spoke and the x-axis.
I know the distance from the origin to where the x-axis enters the rim, apply the Pythagorean theorem to the points calculated last week. Call it d.
I will set the depth of the hole in the hub for the tip of the spoke. Call it t.
And for each run I will enter the y coordinate for where the top side of the spoke enters the rim. Then the distance from the origin up the y-axis to the top of the hub is one half the distance between the ends of the hub minus the input value of y for the spoke at the rim. Call it h.
The next diagram takes the x-y plane from the red coordinates in the cut-away diagram and adds in a short segment of the line across the end of the hub, line y = h, and the line along the top side of the spoke, line ACB. Under it is the derivation of a trigonometric formula for the angle of the spoke.
I labeled the picture of the wheel with the points in the geometry diagram.
A - is on the inside of the rim where the top of the spoke enters the rim
B - is on the face of end of the hub where the spoke would break out of the hub
D - is at the outer circumference on the end of the hub
C - is on the side of the hub where the top of the spoke enters the hub
O - is on the side of the hub, its distance from the end of the hub is variable as I try different amounts of cross over between the outside and inside sets of spokes. It is input as the y coordinate in the POVray coordinates where the top side of the spoke enters the rim.
The distance from O to A we have from last week's work. We calculated the coordinates of the spoke's end points on the plane, use the Pythagorean theorem to calculate the distance, 'd', between them.
d = SQRT((Xrim - Xhub)^2 + (Zrim - Zhub)^2)
The distance from O to D is one half the hub length minus the y coordinate of the offset at the rim. If the offset is to -1/8" and the hub is 1/2" long then this height , h = 1/2 * 1/2 -(-1/8) = 3/8".
The distance B to C, t, is set to 1/32".
What I'm after is the angle OAC which will also be needed in designing the jig for drilling the spoke holes. I think I've broken down the steps fine enough in the diagram for you to follow how I got my formula for the angle. Lets rename angle OAC as just 'a' so the formula reads:
d * tan(a) + t * sin(a) - h = 0
I poked around on http://mathworld.wolfram.com and some other math sites for a solution to this equation but trigonometric equations do not often have easy solutions. This was not one of the easy ones. Having been programming computers for over 40 years I thought of building a binary search program, but in case there was something better I asked for help on the Google group mog-group. Brent Meeker responded with two possibilities. The first idea involved using some trigonometric transformations to eliminate the tan(a) and turn this equation into a quartic equation in sin(a). After looking at the Wolfram site's instructions for solving a quartic equation I had to agree with Brent that this is not the way to do it. His better idea is an iterative approach called, fixed point iteration.
Starting with the fact that tan(a) = sin(a)/cos(a) Brent reworked my formula to calculate the error in a guess of the answer. Here I just paste his explanation.
Instead guess a value of a and solve for the amount of error e in your guess. First multiply thru by cos so you have
d*sin(a) - h*cos(a) + t*sin(a)cos(a) =0
or using a trig identity
d*sin(a) - h*cos(a) + 0.5*t*sin(2a) =0
Then substitute in your guess which is (a-e)
d*sin(a-e) - h*cos(a-e) + 0.5*t*sin(2a-2e) =0
or using trig identities
d*[sin(a)cos(-e)+cos(a)sin(-e)] - h*[cos(a)cos(-e)-sin(a)sin(-e)] +
0.5*t*[sin(2a)cos(-2e)+sin(-2e)cos(2a)]=0
And then here's the payoff. For small angles e, sin(e)=e and cos(e)=1. So you assume you're close and e is small so the above equation becomes
d*[sin(a) -e*cos(a)] - h*[cos(a)+e*sin(a)] + 0.5*t*[sin(2a)-2e*cos(2a)]=0
Which you easily solve for e.
e={d*sin(a) - h*cos(a) + 0.5*t*sin(2a)}/{cos(a) + h*sin(a) +t*cos(2a)}
You add this value to your estimate, which was a-e, and you will have a new value much closer to the true value of a. Take this new value as a new guess and repeat the above calculation of a new e. This should converge very quickly to as much accuracy as you need.
I tried this in a spreadsheet with d = 0.5, h = 0.35, t = 0.03, and a first guess of 45 degrees. But I found I needed to subtract e from the guess not add, maybe because POVray's angles turn backwards to the mathematical convention.
a e
45 17.8768435793
27.1231564207 2.2868135347
24.836342886 0.4709482886
24.3653945974 0.0993094122
It homed in to greater accuracy than any protractor I have in just 4 steps. And it can be coded in a simple while loop containing just two lines of code.
Now that I have the angle a, we can find the point C, it is t * sin(a) in from the end of the hub. But to draw this spoke we need its centre line, line AC is on the side of the spoke.
Adding the spoke centre line to the diagram we can calculate how far it is down to the centre.
The centre line is {Spoke Radius / cos(a)} below the line AC.
Now we can calculate POVray's Y coordinates for the spoke. At the hub it will be
Yhub = 0.5 * Hub Width - t * sin(a) - Spoke Radius / cos(a)
At the rim it will be
Yrim = The input Offset from Centre - Spoke Radius / cos(a)
Of course the spokes on the other side of the hub will have some signs changed. At the hub it will be
Yhub = -0.5 * Hub Width + t * sin(a) + Spoke Radius / cos(a)
and at the rim
Yrim = The input Offset from Centre + Spoke Radius / cos(a)
Now we have the x, y, and z coordinates for the ends of the outer sets of spokes. The inner sets which cross behind the outer ones will have the same angle to the plane of the wheel as their pair mates. To avoid hitting their mates they must be inset by at least:
Spoke Diameter / cos(a)
This amount works OK for the spokes on the narrow end with their shallow angle but I had to increase the inset on the other end's more steeply angled spokes, 1.1 times did the trick. POVray's intersect function clearly shows where any spokes intersect. After playing with the offsets at the rim to get no intersect pieces showing I removed the intersect function to make the following stereoscopic picture of the wheel.
Look through this picture to merge the images and get the 3D effect. It may help to thumb your nose at the picture so each eye see only the image on its side and/or shrink the picture's window a little.
I see I will have to bevel the corner where the hub widens so the spokes from the narrow end can clear it.
Saturday, 5 January 2013
Designing Wooden Model Wire Wheels (Part 1)
Instead of bearing down and getting done cleaning up the finish on the DHC I've been working on a design for the next set of "wire" wheels. My daughter saw what I was doing while here visiting over Christmas and told me I should post the calculations on the blog. So here is why I studied math in high school.
For two reasons I decided to separate the wheels from the tires in this design. One, it lets me use a white hardwood for the wheel and a dark wood for the tires. Two, the wider tire profile used on more recent cars would cause the spoke holes to exit the sides of the tire at a shallow angle which could made drilling awkward. The wire wheel I chose to model has a hub with different diameters at opposite ends and twice as many spokes on the large end as on the small end. In the POVray model I built a hub with a 3/8" diameter axle hole and scaled the rest of the hub around that hole. The rim diameter was scaled to fit in a 2 1/2" diameter tire.
This week I'll just develop the two dimensional weaving pattern of the spokes. The example I'm using has 48 spokes, this is the smallest number that has all the spokes angling into the hub and not just grazing the surface.
On the hub's large diameter end we have 32 spokes. Draw 32 radii around the wheel. To be able to use symmetry to get the second set of spokes rotate the radii one half of the angle between two adjacent radii so the x and y axes bisect the angle between radii.
On the real wire wheels each spoke on the large end of the hub crosses three other spokes from the large end before it reaches the rim. The relatively fatter wooden spokes on the model would not fit across three others so I tried two. Therefore, a spoke at one radius line on the hub will attach to the rim two radii away from its hub radius.
Calling the angle between two adjacent radii a, the hub radius h, and the inside rim radius i, we can calculate the end points of the spokes (Xh, Yh) at the hub and (Xr, Yr) at the rim.
POVray has angles increase in the clockwise direction, opposite to the convention in geometry. Measuring the angle from the twelve o'clock position.
For the spoke angling up to the right:
Xh = h * sin(0.5*a)
Yh = h * cos(0.5*a)
Xr = i * sin(2.5*a)
Yr = i * cos(2.5*a)
By symmetry the ends of the spoke angling to the left are (-Xh, Yh) and (-Xr, Yr).
With the POVray model I do not need to calculate for all the spokes. I can rotate this pair around the centre to fill in the wheel.
The small end of the hub has 16 spokes and each spoke crosses one other spoke. Therefore, the angle between these radii is two times the angle between the radii on the large end, i.e 2*a.
For the spoke angling up to the right:
Xh = h * sin(-a)
Yh = h * cos(-a)
Xr = i * sin(a)
Yr = i * cos(a)
By symmetry the ends of the spoke angling to the left are (-Xh, Yh) and (-Xr, Yr).
Rotating this pair around the wheel we get;
Put the large end spokes together with the small end spokes;
If I wanted to get real ambitious here is a 60 spoke wheel;
Next week I'll add the third dimension, calculating the angle the spokes make with the plane of the wheel.
For two reasons I decided to separate the wheels from the tires in this design. One, it lets me use a white hardwood for the wheel and a dark wood for the tires. Two, the wider tire profile used on more recent cars would cause the spoke holes to exit the sides of the tire at a shallow angle which could made drilling awkward. The wire wheel I chose to model has a hub with different diameters at opposite ends and twice as many spokes on the large end as on the small end. In the POVray model I built a hub with a 3/8" diameter axle hole and scaled the rest of the hub around that hole. The rim diameter was scaled to fit in a 2 1/2" diameter tire.
This week I'll just develop the two dimensional weaving pattern of the spokes. The example I'm using has 48 spokes, this is the smallest number that has all the spokes angling into the hub and not just grazing the surface.
On the hub's large diameter end we have 32 spokes. Draw 32 radii around the wheel. To be able to use symmetry to get the second set of spokes rotate the radii one half of the angle between two adjacent radii so the x and y axes bisect the angle between radii.
On the real wire wheels each spoke on the large end of the hub crosses three other spokes from the large end before it reaches the rim. The relatively fatter wooden spokes on the model would not fit across three others so I tried two. Therefore, a spoke at one radius line on the hub will attach to the rim two radii away from its hub radius.
Calling the angle between two adjacent radii a, the hub radius h, and the inside rim radius i, we can calculate the end points of the spokes (Xh, Yh) at the hub and (Xr, Yr) at the rim.
POVray has angles increase in the clockwise direction, opposite to the convention in geometry. Measuring the angle from the twelve o'clock position.
For the spoke angling up to the right:
Xh = h * sin(0.5*a)
Yh = h * cos(0.5*a)
Xr = i * sin(2.5*a)
Yr = i * cos(2.5*a)
By symmetry the ends of the spoke angling to the left are (-Xh, Yh) and (-Xr, Yr).
With the POVray model I do not need to calculate for all the spokes. I can rotate this pair around the centre to fill in the wheel.
The small end of the hub has 16 spokes and each spoke crosses one other spoke. Therefore, the angle between these radii is two times the angle between the radii on the large end, i.e 2*a.
For the spoke angling up to the right:
Xh = h * sin(-a)
Yh = h * cos(-a)
Xr = i * sin(a)
Yr = i * cos(a)
By symmetry the ends of the spoke angling to the left are (-Xh, Yh) and (-Xr, Yr).
Rotating this pair around the wheel we get;
Put the large end spokes together with the small end spokes;
If I wanted to get real ambitious here is a 60 spoke wheel;
Next week I'll add the third dimension, calculating the angle the spokes make with the plane of the wheel.
Subscribe to:
Posts (Atom)